Least cost feed rations on your personal computer
Mathematical programming models are routinely used to calculate everything from minimum-cost feed rations to scheduling plane flights and blending petroleum products in refineries. A revolution in the software necessary to solve these powerful models has occurred in the past couple of years. Now anyone owning the latest version of most commercial spreadsheets such as Microsoft Excel or Quattro Pro has computational power which only Fortune 500 companies possessed a decade ago. Putting this enhanced computational power to work, however, requires the ability to put together a useful mathematical programming model.
All mathematical programming models have two critical elements: something to be maximized or minimized, and constraints or limitations which reflect production requirements and the availability of resources. In the minimum- cost feed ration, the costs of mixing a nutritional feed are minimized. The constraints in the feed mix problem are the nutritional requirements necessary to maintain good health and assure weight maintenance or gain.
Once the objective to be maximized or minimized is identified, the constraints or limitations directly affecting the objective must be recognized. Most constraints identify scarce resources and biological, physical, or financial requirements. Scarce resources are often easily recognized. In a grazing operation, the extent of available range land limits the number of head that can be grazed. The number of acres a farmer owns and leases limit the area planted in crops. Biological, physical, and financial requirements are sometimes more difficult to quantify. Finding the nutritional requirements for targeted weight gain may not be easy. Determining the proper fertilizer dosage for the targeted yield may require some searching.
A SIMPLE EXAMPLE
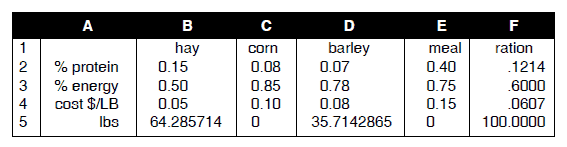
Most real life problems involve many complex interrelationships. The simple example presented here should give you an idea of the kinds of problems which could be solved. The details of the example are necessarily simplified. The problem is the classic feed mix problem. The objective is to find a feed formulation that meets given nutritional requirements at minimum cost. Our possible ingredients are hay, corn, barley and meal. Their nutritional analysis is as shown in the spreadsheet table below.
The hay used for this simple example is assumed to have 15 percent protein and 50 percent TDN by weight. The nutritional analysis for corn, barley and meal are 8, 7, and 40 percent protein and 85, 78, and 75 percent TDN, respectively. A simple spreadsheet can be set up to calculate the protein energy and cost of any possible ration by simply defining the appropriate formulas for the ration column. If % protein is in A2 then a formula of: (B2*B$5+C2*C$5+ D2*D$5+E2*E$5)/F$5 will define the % of protein in the ration and if copied down will mutate to define the % energy and cost per pound as well. The pounds in ration (F5) is simply the sum of the pounds of each individual ingredient, i.e., (B5+C5+D5+E5).

Once you have this simple spreadsheet set up you could then simply try different combinations of ingredients until you found a combination of ingredients that met the nutritional requirements at a reasonable cost. Such a solution is shown in the above table. However, this brute force approach might take a fair amount of time.
A much better way is to use the “solver” option of your spreadsheet. The mechanics of using this option in Microsoft Excel are as follows: (other brands of spreadsheets with solver options have very similar mechanics)
1. Set up your spreadsheet to calculate the necessary values, as described above.
2. Choose the Solver Option from the menu.
3. Enter the cell you want to minimize in the Set Cell Box (F4, ration cost per pound).
4. Click on the Minimize Button.
5. Enter the cells you want to solve for in the By Changing Cells Box (B5:E5, the pounds of possible ingredients).
6. Add the following constraints by clicking on the Add Button:
F2 > = .12 (Protein level must be greater than or equal to 12 percent)
F3 > = .60 (Energy level must be greater than or equal to 60 percent)
F5 = 100 (You want to mix 100 pounds of ration)
B5:E5 > = 0(Negative weights are hard to measure out in formulating a ration. This insures only positive or zero values)
At this point, you have told the computer what cell describes your objective function (F4). You have given it instructions to minimize this value subject to a set of constraints by varying the amount of the various ingredients in your ration. Click on solve and the computer should return the following results.
As you can see, the computer found a cheaper ration meeting all requirements than was found by simply fiddling with the original spreadsheet. Further, additional information is available in the form of a sensitivity report.
What is a Reduced Gradient or a Lagrange Multiplier?
These terms are just techno babble for expressing what happens if you make a small adjustment to the optimum solution the computer found. For example, if you were to add one pound of meal to the solution and let the computer recalculate the ration so that the original constraints were still met the cost per pound of this modified ration would be .000732134 $/lb higher than the original ration. Adding a pound of corn would increase the cost even less. If instead of adjusting the ingredients you made small changes in the constraints the Lagrange multipliers indicate how the optimum cost would change.
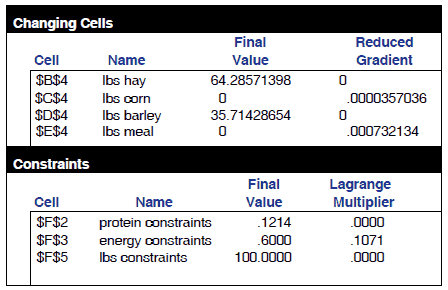
For example a small increase in the protein requirement (say to 12.1 percent) would not change the cost at all. This is because the optimal solution already has more than 12.1 percent protein. A larger change to any value above 12.4 percent would increase the cost and the model would need to be re-optimized to calculate the new optimum and its associated new sensitivity values. Increasing the energy requirement to .61 percent would raise the ration cost .001071 $/lb. (We raised the constraint by .01 units so we must multiply the Lagrange multiplier by .01.)
Could this mathematical modeling stuff be of any real use on a ranch? Is it as easy as the simple model above? The answer to the first question is yes. The simple ration mix problem might even be useful on your ranch. The answer to the second question is Nope. Even the simple ration problem becomes more complex in reality. For example, are the analyses based on dry matter weights or at the feed scale weights? How many different ingredients are reasonable to consider? Most importantly, how should I decide on what the protein, energy, minerals, etc. content of the ration should be. The bottom line is that the current high end spreadsheets have capabilities to help you think about and solve some of the management problems common in ranching today.
by Russell Gum and Gary Thompson - Arizona Cooperative Extension
This article hasn't been commented yet.


Write a comment
* = required field